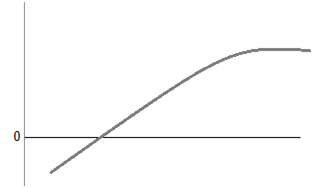
Veámoslo en un gráfico:
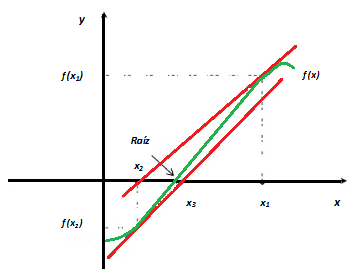 >> Pensemos en una función f(x) y queremos hallar su raíz. Para
ello, escogemos un valor x2, cercano a la raíz de la función, y
trazamos una recta tangente que pasará por el punto x2, f(x2). Ese
punto, nos dará un nuevo valor x2, que es más cercano a la raíz que
queremos calcular.
>> Pensemos en una función f(x) y queremos hallar su raíz. Para
ello, escogemos un valor x2, cercano a la raíz de la función, y
trazamos una recta tangente que pasará por el punto x2, f(x2). Ese
punto, nos dará un nuevo valor x2, que es más cercano a la raíz que
queremos calcular.
Ahora nos preguntamos, vale, pero, ¿Cómo hallo x2? No es problema, gracias a la ecuación punto pendiente:
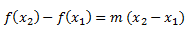
Para que x2 sea una raíz de f(x), f(x2) tendrá que ser igual a 0, si os confunde esto, sustituid f(x2) por “y”; el enunciado quiere decir, hacemos y=0 para poder hallar x2:
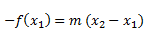
Ahora tomamos “m” como f´(x2), pues al ser la pendiente de la recta tangente a la función en el punto x2, f(x2) nos dará una mejor aproximación:
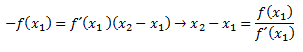
Despejamos x2:
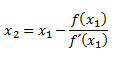
Si queremos generalizar, nos quedará:
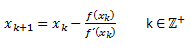
La ecuación resultante en la que se conoce como Ecuación Newton-Raphson.
Ejemplo:
>> Aplicando el método de Newton-Raphson, encontrar una raíz próxima a para la ecuación:
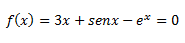
Redondear los cálculos a 5 cifras significativas e iterar hasta que se cumpla
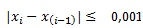
Primero hemos aplicado el Teorema de Bolzano, que si bien, no está directamente relacionado, nos permite comprobar que dicha función existe y es continua en el intervalo [0,1]. Por motivos organizativos, lo dejaremos sin desarrollar, pues ya se hablará de él en otro artículo más extensamente.
Recordamos la fórmula de Newton-Raphson:
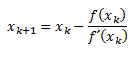
Necesitamos la primera derivada, pasamos a calcularla:
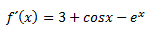
Sustituimos en la fórmula anterior:
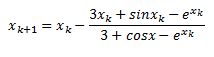
**Pista: Recordad que sin0=1
El dato de referencia(x0) lo elegimos nosotros, con lo cual tomamos x0=0, quedándonos x1=1/3 , x2=0,360170714 y x3=0,36042168 como iteraciones.
Cumplimos la condición del problema ya que:
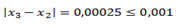
Vemos como quedan las aproximaciones que hemos calculado:
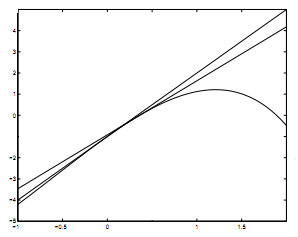
Que son esas dos rectas tangentes que vemos en la gráfica:
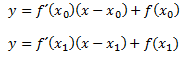
No hay comentarios:
Publicar un comentario